P se ubica en la circunferencia del círculo unitario no deformado x² + y² = 1, y tiene coordenadas (x,y). Tras la deformación yace sobre la elipse de deformación x²/l₁ + y²/l₂ = 1 en el punto P’(x’,y’). El ángulo POx era inicialmente f y a raíz de la distorsión interna es ahora f’. La longitud inicial unitaria de OP ha sido alargada por una extensión de magnitud e y OP’ tiene una elongación cuadrática l. Ya que los ejes de referencia x y y coinciden con las direcciones principales de deformación, las coordenadas de P son modificadas en proporción a las extensiones principales e₁ y e₂; o sea

x’ = xl11/2 y y’ = yl21/2.

(1)

Por otra parte están las relaciones trigonométricas

x = cos f y y = sin f.

(2)

Combinando (1) y (2) tenemos x’ = l₁^1/2 cos f y y’ = l₂^1/2 sin f.
Aplicando el teorema de Pitágoras en el triángulo con hipotenusa OP’ y catetos x’ y y’

l =l1 cos2f + l2 sin2f

(3)

Esta ecuación expresa los cambios de longitud en términos de ángulos medidos en el estado predeformacional. En la mayoría de las situaciones geológicas hacemos mediciones en material deformado, y no conocemos este ángulo. Entonces transformamos esta ecuación para expresar cambios de longitud en términos de f’.
 

x’ = l1/2 cos f’ y y’ = l1/2 sin f’,  cos f = x’/l11/2  y sin f = y’/l21/2.

(4) (5)

Combinando las ecuaciones (4) y (5) tenemos

sin f = l1/2sin f’/l21/2 y cos f = l1/2cos f’/l11/2;

(6)

sustituyendo estos valores en la identidad trigonométrica cos²f + sin²f = 1 y la extensión cuadrática recíproca l’ = 1/l nos da

l’ = l1’cos2f’ + l2’sin2f’.

(7)

Para soluciones gráficas es preferible el diagrama de Mohr, y es más útil expresar (7) en función de 2f usando sustituciones de las identidades de doble ángulo
cos²f = (1 + cos2f)/2 y sin²f = (1 - cos2f)/2
 

.

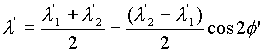(8)

Por otra parte tenemos que existen dos direcciones que son perpendiculares entre sí tanto antes como después de la deformación. En el estado deformado son éstas las direcciones principales de deformación (ejes de la elipse). Estas líneas son evidentemente direcciones sin deformación angular. Todas las otras direcciones inicialmente perpendiculares pierden su ortogonalidad durante la distorsión mediante un ángulo y cuya magnitud depende de la orientación inicial de las líneas así come de la razón axial, R. En la figura se ilustra la tangente al círculo unitario con punto de tangente en P. En el estado deformado la tangente a la elipse es definida por la ecuación

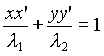
reemplazando a x’ y y’ tenemos

x cos f/l₁^1/2 + y sin f/l₂^1/2 = 1.

Esta tangente ya no es perpendicular a OP, y una línea OQ trazada al origen perpendicular a la tangente nos da la medida del ángulo de cizalla y. La fórmula de la distancia del origen a una recta ax + by = c es p = c/(a² + b²)^1/2 y ahora calculamos este ángulo y en el triángulo P’OQ sabiendo que OP’ tiene longitud l^1/2

.

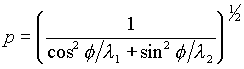En el triángulo P’OQ secy = l^1/2/p = l^1/2(cos²f/l₁ + sin²f/l₂)^1/2

Por la definición de la deformación angular g = tan y

g² = tan²y = sec²y - 1 = l(cos²f/l₁ + sin²f/l₂) - 1 lo cual sustituyendo por l (ecuación 3) y usando la identidad cos²f + sin²f = 1 rinde

.

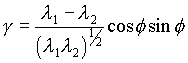De nueva cuenta se encuentra esta ecuación en términos de f y nos interesa en términos de f’. Sustituimos de la ecuación (6)

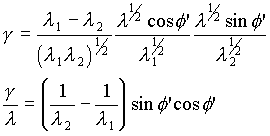
Definiendo g’=g/l y usando la identidad sinf’cosf’ = (sin2f’)/2 obtenemos el resultado

,

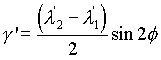(9)

Las ecuaciones (8) y (9) son paramétricas para un círculo en coordenadas rectangulares con centro en l'= (l'₂+l'₁)/2 y radio (l'₂-l'₁)/2.
Esta construcción es completamente análoga a aquella de la construcción del círculo de Mohr para esfuerzos. De hecho cualquier tensor de orden 2 puede ser representado por un círculo de Mohr.
La utilidad del círculo de Mohr para el estado deformado radica en la posibilidad que ofrece para reconstruir la forma del elipse de distorsión interna de un plano utilizando solamente relaciones angulares (ver tarea2).
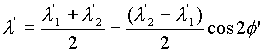
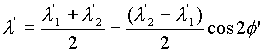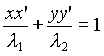
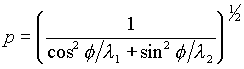
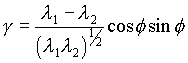
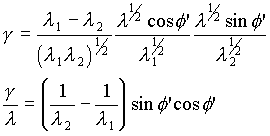
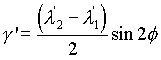